Softmax 的相关知识总结
原文: https://zhuanlan.zhihu.com/p/406751969
Softmax 函数
Softmax 函数与交叉熵_behamcheung 的博客 - CSDN 博客简单易懂的 softmax 交叉熵损失函数求导_绝望的乐园 - CSDN 博客_softmax 损失函数
这篇文章是以上链接中知识点的整理和汇总,方便大家阅读学习。
背景与定义
在 Logistic regression 二分类问题中,我们可以使用 sigmoid 函数将输入 Wx+b 映射到 (0,1) 区间中,从而得到属于某个类别的概率。将这个问题进行泛化,推广到多分类问题中,我们可以使用 softmax 函数,对输出的值归一化为概率值。
这里假设在进入 softmax 函数之前,已经有模型(一般都是全连接层)输出 C 个值,其中 C 是要预测的类别数,模型可以是全连接网络的输出 a,其输出个数为 C,即输出为 a1, a2, ..., aC。下面是一个全连接其中的一个节点的示意图:
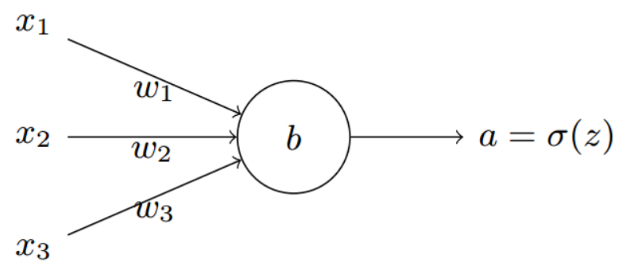
所以对每个样本,它属于类别 i 的概率为:
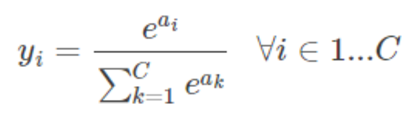
通过上式可以保证所有 yi 的值相加为 1,即属于各个类别的概率和为 1,所以说成为一个归一化的概率值。
性质
由上面的定义就可以看到,softmax 的作用就是将一个序列,变成相应的概率,并且满足如下的条件:
- 所有的概率值都是 [0, 1] 之间。
- 所有的值相加起来是 1。
softmax,顾名思义就是 soft 版本的 max。我们来看一下为什么?
举一个例子,假如 softmax 的输入是:[1.0, 2.0, 3.0];
softmax 的输出结果是:[0.09, 0.24, 0.67];
我们稍微改变一下输入,把 3 改大一点,变成 5,即输入是:[1.0, 2.0, 5.0];
则最终 softmax 的输出会变为: [0.02, 0.05, 0.93]。
可见 softmax 是一种非常明显的 “马太效应”:强(大)的更强(大),弱(小)的更弱(小)。假如你要选一个最大的数出来,这个其实就是叫 hardmax。那么 softmax 呢,其实真的就是 soft 版本的 max。
这种 soft 版本的 max 在很多地方有用的上。因为 hard 版本的 max 好是好,但是有很严重的梯度问题,求最大值这个函数本身的梯度是非常非常稀疏的(比如神经网络中的 max pooling),经过 hardmax 之后,只有被选中的那个变量上面才有梯度,其他都是没有梯度。这对于一些任务(比如文本生成等)来说几乎是不可接受的。
导数
对 softmax 求导数,就是求第 i 项的输出对第 j 项输入的偏导:
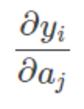
由于 softmax 有多个输出,因此会出现 i 和 j 。代入 softmax 函数表达式,可以得到:
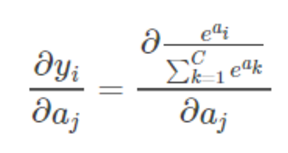
其中再次强调,由于 softmax 公式的特性,它的分母包含了所有神经元的输出,所以,上式的求导过程要分情况讨论:
-
如果
,则
对
求导的结果为
;
-
如果
,则
对
求导的结果为 0。
并且
对
的求导结果总是
。
所以说,当
的时候:
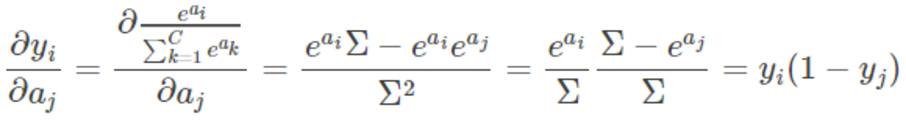
当
的时候:
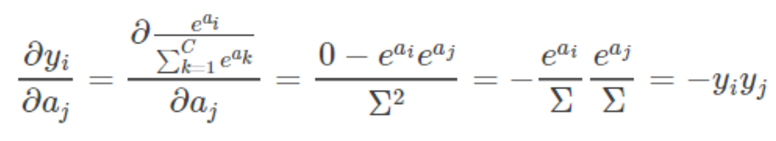
softmax 的计算与数值稳定性
在 python 中,softmax 的函数实现为,注意这里全部都是向量计算:
def softmax(x):
exp_x = np.exp(x)
return exp_x / np.sum(exp_x)
传入 [1, 2, 3, 4, 5] 的向量
>>> softmax([1, 2, 3, 4, 5])
array([ 0.01165623, 0.03168492, 0.08612854, 0.23412166, 0.63640865])
但如果输入值较大时:
>>> softmax([1000, 2000, 3000, 4000, 5000]) array([ nan, nan, nan, nan, nan])
这是因为在求 exp(x) 时候溢出了:
import math
math.exp(1000)
# Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
# OverflowError: math range error
一种简单有效避免该问题的方法就是让 exp(x) 中的 x 值不要那么大或那么小,在 softmax 函数的分式上下分别乘以一个非零常数:
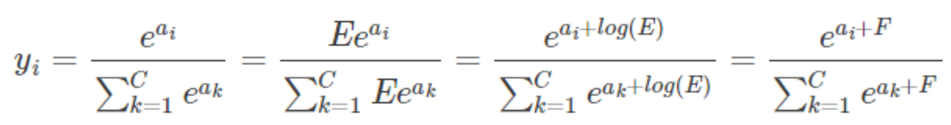
这里 log(E) 是个常数,所以可以令它等于 F 。加上常数 F 之后,等式与原来还是相等的,所以我们可以考虑怎么选取常数 F。我们的想法是让所有的输入在 0 附近,这样
的值不会太大,所以可以让 F 的值作为输入数据的最大值的相反数:
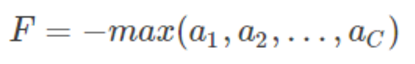
这样子将所有的输入平移到 0 附近(当然需要假设所有输入之间的数值上较为接近),同时,除了最大值,其他输入值都被平移成负数,e 为底的指数函数,变量越小函数值越接近 0,这种方式比得到 nan 的结果更好。
我们可以这样子修改 softmax 函数:
def softmax(x):
shift_x = x - np.max(x)
exp_x = np.exp(shift_x)
return exp_x / np.sum(exp_x)
从新计算可以得到:
>>> softmax([1000, 2000, 3000, 4000, 5000])
array([ 0., 0., 0., 0., 1.])
当然这种做法也不是最完美的,因为 softmax 函数不可能产生 0 值,但这总比出现 nan 的结果好,并且真实的结果也是非常接近 0 的。
这样一种实现数值稳定性已经好了很多,但是仍然会有数值稳定性的问题。比如输入的值差别过大的时候,比如 [-1000, 1, 1000]。这种情况即使用了上面的方法,可能还是报 nan 的错误。但是这个就是数学本身的问题了,大家使用的时候稍微注意下。
一种可能的替代的方案是使用 LogSoftmax(然后再求 exp),数值稳定性比 softmax 好一些。如下所示,可以看到,LogSoftmax 省了一个指数计算,省了一个除法,数值上相对稳定一些。另外,其实 Softmax_Cross_Entropy 里面也是这么实现的。
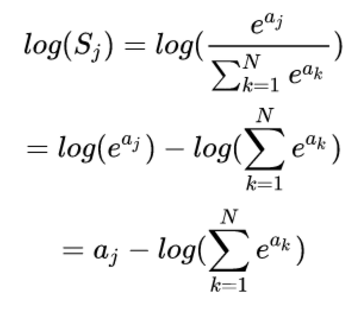
Softmax 与 Sigmoid 的区别
Sigmoid = 多标签分类问题 = 多个正确答案 = 非独占输出(例如胸部 X 光检查、住院)
我们先来回忆一下 sigmoid 的计算和相应的函数图形如下所示:
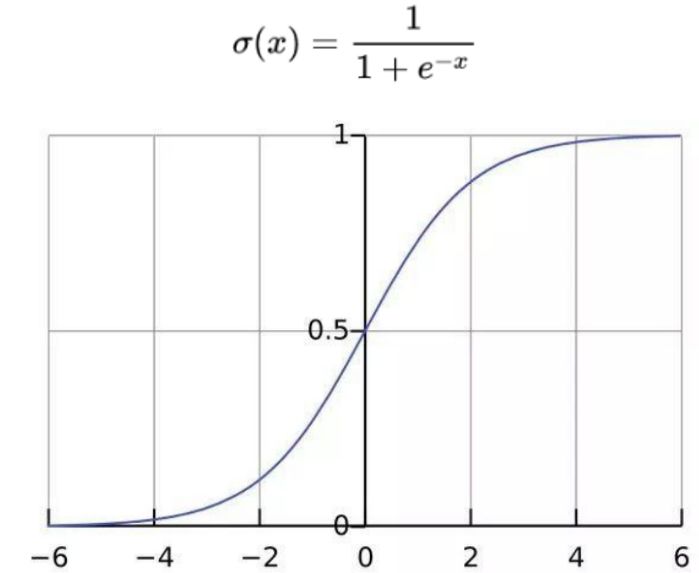
由于 Sigmoid 函数分别应用于每个原始输出值,因此可能出现的输出情况包括:所有类别概率都很低(如 “此胸部 X 光检查没有异常”),一种类别的概率很高但是其他类别的概率很低(如 “胸部 X 光检查仅发现肺炎”),多个或所有类别的概率都很高(如 “胸部 X 光检查发现肺炎和脓肿”)。
Softmax = 多类别分类问题 = 只有一个正确答案 = 互斥输出(例如手写数字)
构建分类器,解决只有唯一正确答案的问题时,用 Softmax 函数处理各个原始输出值。 Softmax 函数的分母综合了原始输出值的所有因素,这意味着,Softmax 函数得到的不同概率之间相互关联。详细的对比参考 这里 。
交叉熵损失函数
推导:最小化交叉熵损失等价于最大化对数似然
二分类交叉熵的推导:logistics regression.note,对于多分类交叉熵来说,性质是一样的,可以参考:https://blog.csdn.net/ccj_ok/article/details/78066619
相对熵
说交叉熵之前先介绍相对熵,相对熵又称为 KL 散度(Kullback-Leibler Divergence),用来衡量两个分布之间的距离,记为
,如下所示,其中 H(p) 是 p 的熵。
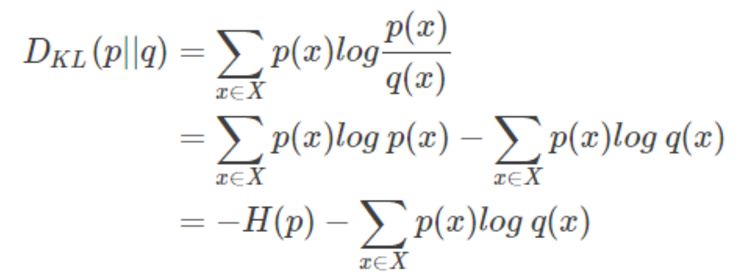
交叉熵损失函数
假设有两个分布 p 和 q ,它们在给定样本集上的交叉熵定义为:
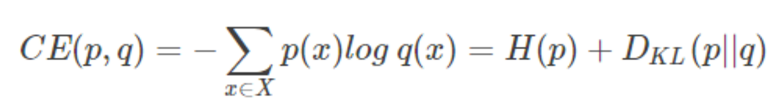
从这里可以看出,交叉熵和相对熵相差了 H(p),而当 p 已知的时候,H(p) 是个常数,所以交叉熵和相对熵在这里是等价的,反映了分布 p 和 q 之间的相似程度。关于熵与交叉熵等概念,可以参考该 博客 再做了解。
回到我们多分类的问题上,真实的类标签可以看作是分布,对某个样本属于哪个类别可以用 One-hot 的编码方式,是一个维度为 C 的向量,比如在 5 个类别的分类中,[0, 1, 0, 0, 0] 表示该样本属于第二个类,其概率值为 1。我们把真实的类标签分布记为 p ,该分布中,t_i = 1 当 i 属于它的真实类别 c。同时,分类模型经过 softmax 函数之后,也是一个概率分布,因为所有的概率和为 1,所以我们把模型的输出的分布记为 q,它也是一个维度为 C 的向量,如 [0.1, 0.8, 0.05, 0.05, 0] 。
对一个样本来说,真实类标签分布与模型预测的类标签分布可以用交叉熵来表示:
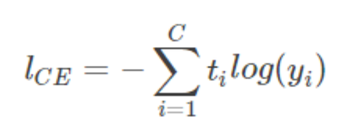
可以看出,该等式于上面对数似然函数的形式一样!我们就称上式为交叉熵损失函数。最终,对所有的样本,我们有以下 loss function,其中 t_{ki} 是样本 k 属于类别 i 的概率,y_{ki} 是模型对样本 k 预测为属于类别 i 的概率。
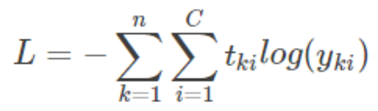
softmax 和 cross-entropy 是什么关系
softmax 和 cross-entropy 本来没有太大的关系,只是把两个放在一起实现的话,算起来更快,数值也更稳定。cross entropy 是用来衡量两个概率分布之间的距离的,softmax 能把一切转换成概率分布,那么自然二者经常在一起使用。
由 cross-entropy 的公式可以看到,这里的 log(y) 就是我们前面说的 LogSoftmax。这玩意算起来比 softmax 好算,数值稳定还好一点。所以说,这有了 PyTorch 里面的 torch.nn.CrossEntropyLoss。这个 CrossEntropyLoss 其实就等于 torch.nn.LogSoftmax + torch.nn.NLLLoss。具体可以看 NLLLoss 和 CrossEntropyLoss.note。
Cross-entropy 求导
对单个样本来说,损失函数
对输入
的导数为:
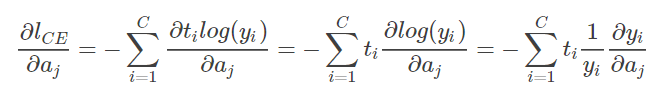

所以,将求导结果代入上式,需要注意的是,针对分类问题,我们给定的结果 t_i 最终只会有一个类别为 1,其他的类别都是 0。